Was sind Typsystembeispiele für lokale Eichtransformations- und Feldstärke-ähnliche Objekte?

Dies ist im Wesentlichen ein Follow-up, das durch diese Antwort auf meine Frage zur Interpretation der Eichtransformation von Identitätstypen motiviert ist.

Ein Feld

ψ : M → C N
ist ein Abschnitt der C N -Bündel über der Raumzeit-Mannigfaltigkeit M . Wir haben eine lokale Messgerättransformation
ψ ( X ) ↦ ψ ' ( X ) := U ( X ) ψ ( X )   :   ( M → C N ) → ( M → C N ) .

Betrachten Sie nun eine Sprache mit Typpolymorphismus und der Klasse M aller Typen, deren Elemente in eine Liste aufgenommen werden können. Lassen Ψ sei die polymorphe Funktion, die für jeden Typ X ∈ M , Karten ein X -list auf eine Ganzzahl, nämlich ihre Länge. Verwenden Sie beispielsweise die Haskell- Syntax, wenn X = B Ö Ö l , Dann Ψ B Ö Ö l ( [ T R u e , T R u e , F A l S e ] ) = 3 . In System-F- Notation haben wir

Ψ : ∀ X . ( [ X ] → ICH N T ) .

Die Spurtransformationen sollten Karten entsprechen

u   :   ∀ X . ( [ X ] → ICH N T )   ⟶   ∀ X . ( [ X ] → ICH N T ) .

Ich könnte mir einige einfallen lassen u 's, zum Beispiel Mapping der Längenfunktion Ψ zu einer Karte Ψ ' := u Ψ was stattdessen die 42-fache Länge einer Liste zurückgibt. Aber das wäre, in physikalischer Hinsicht, eine globale Spurtransformation, weil sie nicht typabhängig ist X . Ich denke, da die einzige Invariante eines endlichdimensionalen Vektorraums seine Kardinalität ist, sollte es in diesem Fall nicht möglich sein, eine lokale Transformation zu konstruieren. Was wäre in diesem Sinne ein praktisches Beispiel für eine lokale Spurweitentransformation?

Außerdem wollte ich einen Alltag parallel zu Identitätstypen zeichnen. Nun, zuerst gibt es das kleine Hindernis, dass die obige Transformation in den meisten Sprachen nicht durch einen Ausdruck gegeben werden kann, da Typen normalerweise keine erstklassigen Objekte sind. Ich denke, diese Designentscheidung wird getroffen, weil sonst die Typinferenz verdorben würde. In der Homotopie-Typentheorie haben Sie die Erkenntnis, dass "Typen auch Begriffe sind" (über n-Kategorien?), Und dann ist es möglich. Aber auf jeden Fall kann ich die Spezifikation immer noch nicht genau festlegen, wenn ein Typ ein Identitätstyp ist . Ich verstehe "Identität" für homotopieäquivalente Räume und eichinvariante Lagrangianer, aber gibt es nicht-geometrische Strukturen, insbesondere programmierungsrelevante,

bearbeiten : Ich habe jetzt zwei Visualisierungen des Beispiels hier und dann gemacht:

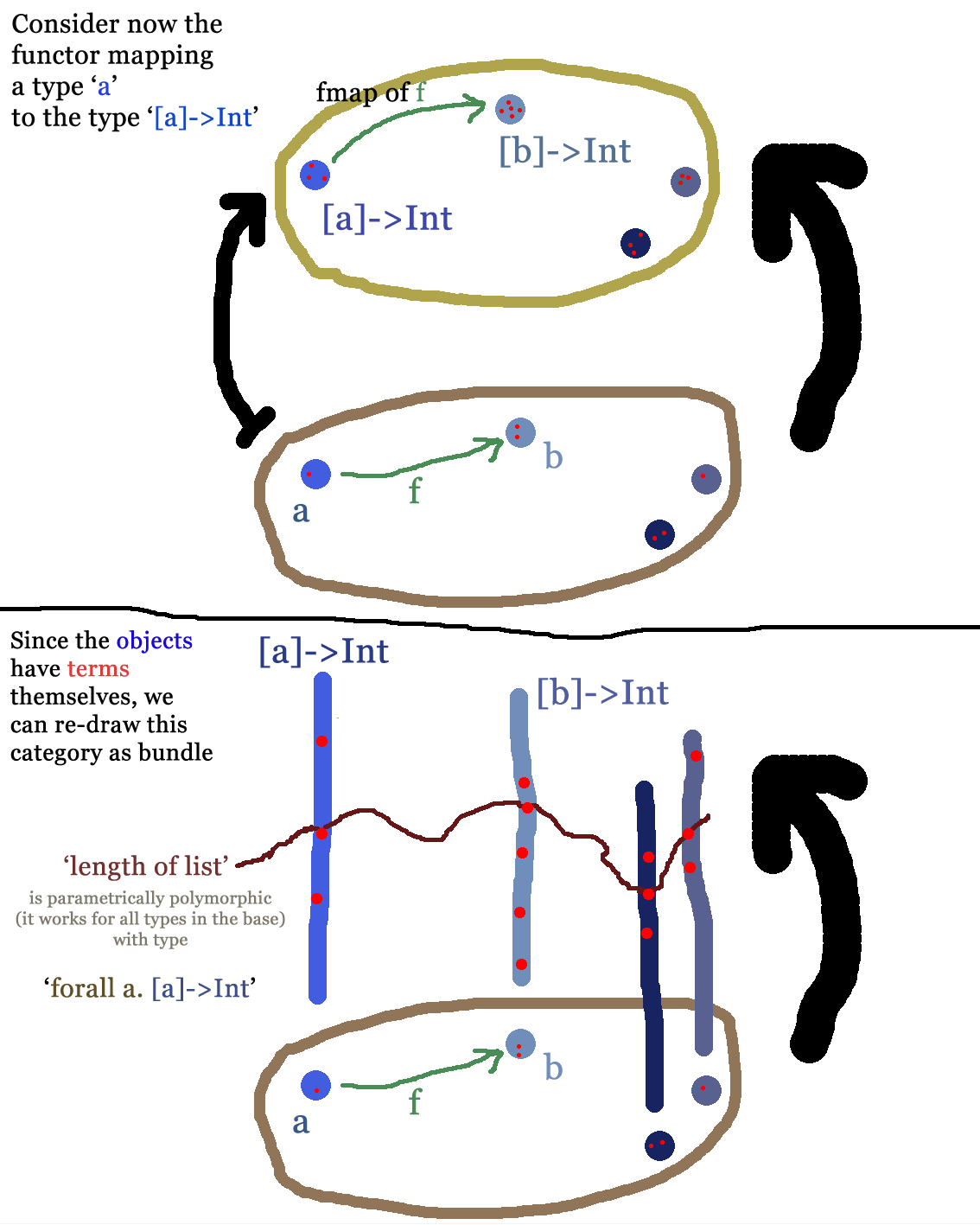
Geben Sie hier die Bildbeschreibung ein

Die Frage ist dann, was ein vernünftiger Maßstab für den Abschnitt im zweiten Bild wäre. (Ich habe auch zwei weitere Bilder gemacht, die über das Gefragte hinausgehen: natürliche Transformationen und Monaden wie in Haskell .)

Übrigens weiß ich, dass HoTT abhängige Typen implementiert , nicht "nur" parametrisch polymorphe, aber das sollte kein Hindernis sein.

Antworten (1)

In der Frage werden sehr unterschiedliche Aspekte angesprochen. Ich werde versuchen, einige Hinweise zu geben. Aber ich bemerke, dass der Bezug dieser Frage zur tatsächlichen Physik nicht sehr stark ist, stattdessen scheint die Frage allgemeiner zu sein, nachdem man ein Gefühl für Identitätstypen in der Homotopietypentheorie (HoTT) bekommen hat. Ich kann mir vorstellen, dass es andere Diskussionsgruppen gibt, die für diese Art von Themen besser geeignet sind, zum Beispiel die Google-Gruppe mit dem (wohl unglücklichen) Titel " HoTT-Amateure ", an die Sie vielleicht denken könnten, Fragen zu stellen.

Nun zu den Fragen, die ich kurz von oben nach unten durchgehe:

zuerst eine Karte M → C N ist ein C N -bewertete Funktion an M . Man kann dies als Abschnitt von a betrachten C N -Faserbündel vorbei M , ja, aber das wäre dann das triviale solche Faserbündel.

(Abschnitte von nicht trivialen Bündeln können in HoTT codiert werden, indem abhängige Typen verwendet werden. Wenn Sie tatsächlich mehr darüber erfahren möchten, lassen Sie es mich wissen, und ich erweitere).

Dann in Bezug auf die Auto-Äquivalenzen des Funktionstyps von Listen zu den natürlichen Zahlen: Ich nehme an, dass dies in der Tat nicht viele Auto-Äquivalenzen haben wird. Wenn man nicht natürliche Zahlen, sondern ganze Zahlen betrachten würde, gäbe es einige offensichtliche (nämlich addieren Sie +1 zu jeder Funktion, deren Umkehrung die Operation wäre, die -1 addiert).

Dann zu der Frage, wie man einen Identitätstyp identifiziert: Man schaut sich nicht einen beliebigen Typ an und fragt: "Ist das ein Identitätstyp?" (Man kann das tun, aber ich glaube nicht, dass Sie danach streben.) Vielmehr konstruiert man für einen gegebenen Typ den entsprechenden Identitätstyp. (Beachten Sie auch, dass der Identitätstyp eines Typs X ist ein X × X -abhängiger Typ. )

Angesichts der Art der obigen Fragen scheint es mir, dass tatsächliche Anwendungen in der Physik nicht so sehr im Mittelpunkt stehen, als vielmehr ein grundlegendes Gefühl für die Homotopietypentheorie als solche zu bekommen. Dazu gibt es meiner Meinung nach nichts Besseres, als das HoTT-Buch durchzuarbeiten . (Ich nehme an, Sie wissen das bereits, aber lassen Sie es mich trotzdem noch einmal betonen.)

Danke für die Antwort. 1) Hinzufügen ± 1 ist wieder global, da es die Typen nicht sieht, aber ich verstehe das jetzt. 2) Ich möchte sehen, warum Messgeräte als Identitätstypen angesehen werden sollten. Sie sagten: "Insbesondere wenn die Homotopie-Typentheorie mit dem zusätzlichen Axiom der differentiellen Kohäsion ausgestattet ist, dann kann man Identitätstypen "differenzieren". Gibt es etwas, was wir von HoTT bekommen, was wir nicht haben, wenn wir noch direkter einen passenden Topos für unsere Physik aufstellen? Dh gibt es einen Grund, warum Typen hier eigentlich im Vorteil sind, abgesehen vom Meta-Vorteil, dass sich mittlerweile viele unterschiedliche Leute dafür interessieren?
Um Ihre Frage zu beantworten: Ja, in HoTT gibt es Eichtransformationen, die in einem gewöhnlichen Topos nicht vorhanden sind. Beispielsweise gibt es im kohäsiven HoTT einen Typ BU(1)_conn von elektromagnetischen Eichfeldern. Das gibt es in keinem einfachen Topos (1-Topos). Für X eine Mannigfaltigkeit, dann ist eine Funktion X --> BU(1)_conn ein elektromagnetisches Eichfeld auf X und eine Homotopie zwischen zwei solchen Abbildungen ist eine Eichtransformation zwischen diesen Feldkonfigurationen. Dieser eichen-/homotopietheoretische Aspekt ist in einem gewöhnlichen Topos nicht vorhanden.
Was sind Typsystembeispiele für lokale Eichtransformations- und Feldstärke-ähnliche Objekte?
AntwortenHierDatenschutz-Bestimmungen1y, 0v